This project studies learning-based, distributed task-allocation algorithms that can handle the complex group dynamics of multi-robot systems.
Tranditional algorithms for task-allocation and scheduling make simplifying assumptions that are not always valid in multi-robot systems. In particular they assume independant tasks, i.e. that the completion time for each task is independant of the general allocation pattern. This does not hold true in groups of robots where in general, assigning more robots to a task means increasing the level of interference, something that leads to a change in the completion time for all the robots involved in that task.
To handle complex group dynamics we use the Vacancy Chain (VC) metaphor commonly used to describe resource allocation in animal and human societies. Complex group dynamics are difficult or impossible to model, so we use a distributed Reinforcement Learning approach to task utility estimation.
A vacancy chain is a social structure through which resources are distibuted to consumers. The typical example is a bureaucracy where the retirement of a senior employee creates a vacancy that is filled by a less senior employee. This promotion, in turn, creates a second vacancy to be filled, and so on. The vacancies form a chain linked by the promotions. The resources that are distributed in this example are the positions, and the consumers are the employees. The general process of distributing resources in this way was originally reported in human populations relating to houses and apartments as well as to jobs in bureaucracies. Chase proposed that major human consumer goods also move through vacancy chains and that such chains are common in other species including the hermit crab, the octopus, and various species of birds.
Chase listed three requirements for resource distribution through vacancy chains:
- The resource to be distributed must be reusable, discrete, and used by only one individual.
- A vacancy is required before an individual takes a new resource unit, and individuals must need or desire new units periodically.
- Vacant resource units must be scarce, and many individuals must occupy sub-optimal units.
This work considers a particular subclass of the general robot task-allocation problem where each sub-task is repeated indefinitely and has a related value.
A sub-task can have any number of robots assigned to it. Assigning a j'th robot to a sub-task is called filling service-slot, j. A particular number of homogeneous robots, j, servicing the same sub-task, i, will have a corresponding task completion frequency, ci,j, dependent on the degree to which they are able to work concurrently without getting in each other's way. The difference in completion frequency together with the sub-task value, vi, define the contribution of the last robot added or the last service-slot filled. We call this contribution, which can be negative, the slot-value, si,j. The formal definition is given below:
si,j=(ci,j-ci,j-1)vi
In these kinds of problems, the group performance is optimized if each robot individually optimizes the value of the service-slot it occupies. This allows us to use distributed optimization algorithms without complex communication structures or centralized decision points.
In a scenario where the service-slots are allocated optimally, a failure in a robot servicing a high-value sub-task will result in an empty high-value service-slot that must be reallocated for optimal system performance. Expressed in the vacancy-chain framework, a vacant, high-value service-slot is a resource to be distributed among the robots.
In the basic transportation problem, a group of robots traverse a given environment in order to transport items between the sources and the sinks. To perform optimally on this task the robots must maximize the number of traversals in general.
The basic transportation problem is one of the sub-problems of foraging If the location of sources and sinks are given, the foraging problem is reduced to a problem of transportation. We have defined the prioritized transportation problem as an extention to the basic transportation problem, where the sources and sinks, the targets of the transportation, into sets of different priority also called different circuits. In the prioritized transportation problem the robot group must strike the correct balance between target utility and robot interference in order to optimize its performance.
Each controller in our experiments had a set of pre-programmed high-level approach behaviors and used Temporal Difference Q-learning to associate different input states with one of these. The Q-tables ware initiated with random values between -0.1 and 0.1, the learning-rate, α, was set to 0.1, and the return discount factor, γ, was set to 0.95. For action selection we used a greedy-ε, strategy where ε was set to 0.1. Because we wanted the system to remain adaptive to changes in the environment we did not decrease ε over time.
In order to demonstrate that our system optimized its performance by distributing tasks through a VC structure, we first show that the group structure and individual robot actions satisfy the definition of a VC process. We then show that this form of TA performs significantly better than random and static TA algorithms.
The experiments took place in a simulated 12x8-meter environment with two sets of sources and sinks. The sources and sinks were simulated laser-beacons, effectively bar-codes made from high-reflection material and recognizable by the laser range finder. We did not require actual objects to be carried. A minimum proximity to a target was interpreted as a delivery or a pick-up. The figure below shows a graphical rendering of the simulated environment in which the experiments took place, with the sources and sinks labeled.

Reward Structure
The robots received a reward, r1, whenever they reached a target in circuit one, i.e., source one or sink one. Correspondingly, they received a reward, r2, whenever they reached a target in circuit two. We call the circuit with the highest related reward the high-value circuit and correspondingly, the the circuit with the lowest related reward is called the low-value circuit. The robots also received an explicit punishment, p, when they were forced to avoid another robot. Robot avoidance was defined as the combination of a minimum laser proximity and presence of color markings.Initial Task Distribution
This set of experiments used six robots with randomly initialized Q-tables. We did 20 individual, each averaging 3000 traversals. To show the structure that emerged we look at the last target visited by each robot. This gives seven possible system states. We refer to each state using the notation, h:l, where h is the number of robots whose last target was on the high-value circuit. Correspondingly, l is the number of robots whose last target was on the low-value circuit. The two distributions presented below show the amount of time the system spent in each possible state when using a random allocation algorithm and the VC algorithm. The standard deviation is indicated by the error bars for each state.
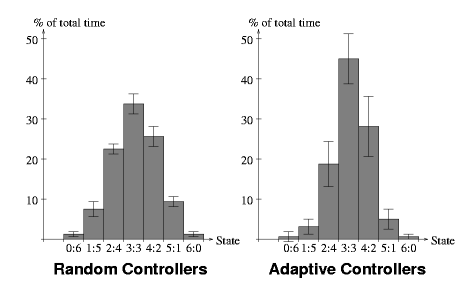
The increase in the amount time the system spends in state 3:3 when using the VC algorithm is statistically significant on a 90% confidence level. The time the adaptive group spends in state 3:3 is also significantly higher than the time spent in any of the other states. Together, the distributions show that the adaptive controllers a adopt a dedicated allocation pattern.
Vacancy from Robot Breakdown
The second set of experiments used five robots with Q-tables taken from the end of the initial task distribution experiment. We randomly removed one of the robots dedicated to the high value circuit, thus creating a vacancy on that sub-task. The converged controllers kept the system in state 3:2 for a significantly larger amount of time than a group of five random controllers. The resulting time distribution are given below.
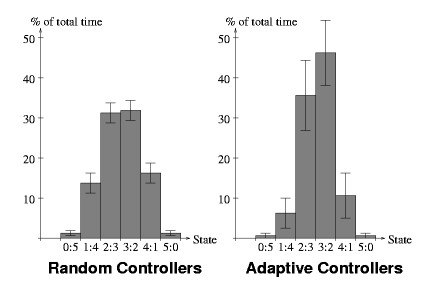
These results show that the group has adapted its structure from one that promotes the 3:3 state to one that promotes the 3:2 state. Such a change implies that a robot from the low-value circuit has filled the vacancy we created in the high-value circuit.
The graph below presents performance data showing that on the removal of a robot from the high-value circuit, the performance drops sharply. After the re-convergence period, however, the performance rises again to a level that is significantly higher than the performance of five random controllers and also significantly higher than the mean performance, over 20 trials, of a group of robots controlled by a static task-allocation algorithm optimized for six robots. The average performance of the static group is indicated by the thin solid line.
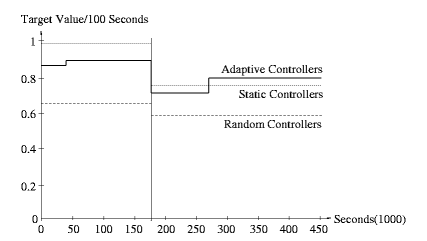
-
[to appear] Torbjørn S. Dahl, Maja J Mataric´ and Gaurav S. Sukhatme, A machine learning method for improving task allocation in distributed multi-robot transportation. To appear in Complex Engineering Systems, Dan Braha, Ali Minai, and Yaneer Bar-Yam (Eds.), Perseus Books, Reading, Massachusetts, 2004. [ps] [pdf]
-
[submitted] Torbjørn S. Dahl, Maja J Mataric´ and Gaurav S. Sukhatme, Multi-Robot Task Allovation through Vacancy Chains. Submitted to (Autonomous Robots), March, 2004. [ps] [pdf]
-
[submitted] Torbjørn S. Dahl, Maja J Mataric´ and Gaurav S. Sukhatme, Emergent Robot Differentiation in Distributed Multi-Robot Task Allocation. Submitted to the 7th International Symposium on Distributed Autonomous Robotic Systems (DARS'04), Toulouse, France, May 23 - 25, 2004. [ps] [pdf]
-
Torbjørn S. Dahl, Maja J Mataric´ and Gaurav S. Sukhatme, Multi-Robot Task Allocation through Vacancy Chains. In the Proceedings of the 2003 IEEE International Conference on Robotics and Automation (ICRA'03), pp2293-2298, Taipei, Taiwan, September 14 - 19, 2003. [ps] [pdf]
The project is funded in part by the Deparment of Energy (DOE), Robotics and Intellgent Machines (RIM), grant number DE-FG03-01ER45905, for "Multi-Robot Learning in Tightly-Coupled, Inherently Cooperative Tasks", and in part by the Office of Naval Research (ONR), Defence University Reseach Instrumentation Program (DURIP), grant number 00014-00-1-0638 for "Equipment Support for Dynamic Adaptive Wireless Networks with Autonomous Robot Nodes".
