 |
||||
| Home | Publications | Miscellaneous | Personal Details | |
|---|---|---|---|---|
 |
||||
| Home | Publications | Miscellaneous | Personal Details | |
|---|---|---|---|---|
|
Project:
|
|---|
This project studies learning-based, distributed task-allocation algorithms that
can handle the complex group dynamics of multi-robot systems.
Tranditional algorithms for task-allocation and scheduling make simplifying
assumptions that are not always valid in multi-robot systems. In particular
they assume independant tasks, i.e. that the completion time for each task is
independant of the general allocation pattern.
This does not hold true in groups of robots where in general, assigning more
robots to a task means increasing the level of interference, something that
leads to a change in the completion time for all the robots involved in that
task.
To handle complex group dynamics we use the Vacancy Chain (VC) metaphor
commonly used to describe resource allocation in animal and human societies.
Complex group dynamics are difficult or impossible to model, so we use a
distributed Reinforcement Learning approach to task utility estimation.
A vacancy chain is a social structure through which resources are distibuted to
consumers.
The typical example is a bureaucracy where the retirement of
a senior employee creates a vacancy that is filled by a less senior employee.
This promotion, in turn, creates a second vacancy to be filled, and so on. The
vacancies form a chain linked by the promotions. The resources that are
distributed in this example are the positions, and the consumers are the
employees.
The general process of distributing resources in this way was originally
reported in human populations relating to
houses and apartments as well as to jobs in bureaucracies. Chase
proposed that major human consumer goods also move through
vacancy chains and that such chains are common
in other species including the hermit crab, the octopus, and various species
of birds.
Chase listed three requirements for resource distribution through vacancy
chains:
This work considers a particular subclass of the general robot task-allocation
problem where each sub-task is repeated indefinitely and has a related
value.
A sub-task can have any number of robots assigned to it.
Assigning a j'th robot to a sub-task is called filling
service-slot, j.
A particular number of homogeneous robots, j, servicing the same
sub-task, i, will have a corresponding task completion frequency,
ci,j, dependent on the degree
to which they are able to work concurrently without getting in each other's way.
The difference in completion frequency together with the
sub-task value, vi, define the
contribution of the last robot added or the
last service-slot filled. We call this contribution, which can be negative, the
slot-value, si,j. The formal
definition is given below:
si,j=(ci,j-ci,j-1)vi
In these kinds of problems, the group performance is optimized
if each robot individually optimizes the value of the service-slot it occupies.
This allows us to use distributed optimization algorithms without complex
communication structures or centralized decision points.
In a scenario where the service-slots are allocated optimally, a failure in a
robot servicing a high-value sub-task will result in an empty high-value
service-slot that must be reallocated for optimal system performance.
Expressed in the vacancy-chain framework, a vacant, high-value service-slot
is a resource to be distributed among the robots.
In the
basic transportation problem, a group of robots traverse a given
environment in order to transport items between the sources and the sinks. To
perform optimally on this task the robots must maximize the number of
traversals in general.
The basic transportation problem is one of the sub-problems of
foraging
If the location of sources and sinks are given, the foraging problem is reduced
to a problem of transportation.
We have defined the prioritized transportation problem as an extention
to the basic transportation problem, where the sources and sinks, the
targets of the transportation,
into sets of different priority also called different circuits.
In the prioritized transportation problem the robot group must
strike the correct balance between target utility and robot interference in
order to optimize its performance.
The experiments took place in a simulated 12x8-meter environment
with two sets of sources and sinks.
The sources and sinks were simulated laser-beacons, effectively bar-codes made
from high-reflection material and recognizable by the laser range finder.
We did not require actual objects to be carried. A minimum proximity to a
target was interpreted as a delivery or a pick-up.
The figure below shows a graphical rendering of
the simulated environment in which
the experiments took place, with the sources and sinks labeled.
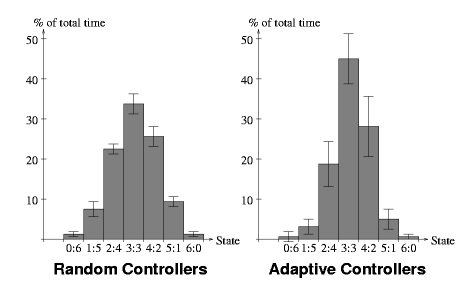
The increase in the amount time the system spends in state 3:3 when
using the VC algorithm is statistically
significant on a 90% confidence level. The time the adaptive group spends in
state 3:3 is also significantly higher than the time spent in any of
the other states.
Together, the distributions show that the
adaptive controllers a adopt a dedicated allocation pattern.
These results show that the group has adapted its structure from one that
promotes the 3:3 state to one that promotes the 3:2 state.
Such a change
implies that a robot from the low-value circuit has filled the vacancy we
created in the high-value circuit.
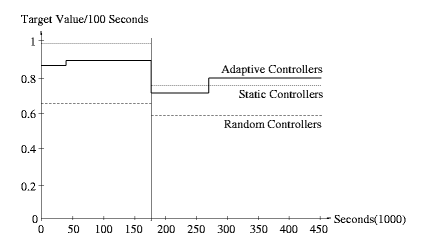
The graph below presents performance data showing that on the
removal of a robot from the high-value circuit, the performance drops sharply.
After the re-convergence period, however, the performance rises again to a level
that is significantly higher than the performance of five random controllers
and also significantly higher than the mean performance, over 20 trials, of a
group of robots controlled by a static task-allocation algorithm optimized for
six robots.
The average performance of the static group is indicated by the thin solid line.
The project is
funded in part by the Deparment of Energy (DOE), Robotics and
Intellgent Machines (RIM), grant number
DE-FG03-01ER45905, for "Multi-Robot Learning in Tightly-Coupled, Inherently
Cooperative Tasks", and in part by the Office of Naval Research (ONR), Defence
University Reseach Instrumentation Program (DURIP), grant number
00014-00-1-0638 for "Equipment Support for Dynamic Adaptive Wireless Networks
with Autonomous Robot Nodes".
Multi-Robot Task-Allocation through Vacancy Chains
Research Objectives
Vacancy Chains
Vacancy Chains for Task Allocation
The Prioritized Transportation Problem
Adaptive Controllers
Each controller in our experiments had a set of pre-programmed high-level
approach behaviors and used Temporal Difference Q-learning
to associate different input states with one of these.
The Q-tables ware initiated with random values between -0.1 and
0.1, the
learning-rate, α, was set to 0.1, and the return
discount factor, γ, was set to 0.95.
For action selection we used a greedy-ε, strategy where
ε was
set to 0.1. Because we wanted the system to remain adaptive to changes
in the environment we did not decrease ε over time.
Experimental Setup
In order to demonstrate that our system optimized its performance by
distributing tasks through a VC structure, we first show that the
group structure and individual robot actions satisfy the definition of a
VC process. We then show that this form of TA
performs significantly better than random and static TA algorithms

Reward Structure
The robots received a reward, r1, whenever they reached a
target in circuit one, i.e., source one or sink one.
Correspondingly, they received a reward, r2, whenever they
reached a target in circuit two.
We call the circuit with the highest related reward the
high-value circuit and correspondingly, the the circuit with the lowest
related reward is called the low-value circuit.
The robots also received an explicit punishment, p, when they were forced to avoid
another robot. Robot avoidance was defined as the combination of a minimum
laser proximity and presence of color markings.
Results
Initial Task Distribution
This set of experiments used six robots with randomly initialized Q-tables.
We did 20 individual, each averaging 3000 traversals.
To show the structure that emerged we look at the last target visited by each
robot. This gives
seven possible system states. We refer to each state using the notation,
h:l,
where h is the number of robots whose last target was on the high-value
circuit. Correspondingly, l is the number of robots whose last target
was on the low-value circuit.
The two distributions presented below show the amount of time the system
spent in each possible
state when using a random allocation algorithm and the VC algorithm.
The standard deviation is indicated by the error bars for each state.
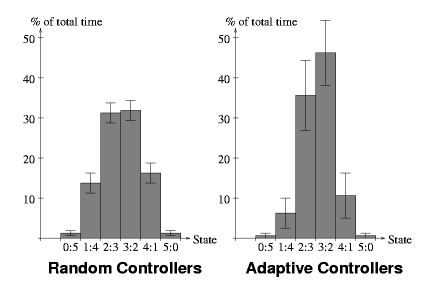
Vacancy from Robot Breakdown
The second set of experiments used five robots with Q-tables taken from the
end of the initial task distribution experiment. We randomly removed one of
the robots dedicated to the high value circuit, thus creating a
vacancy on that sub-task.
The converged controllers kept the system in state 3:2 for a
significantly larger amount of time than a group of five random controllers.
The resulting time distribution are given below.
Publications
Return to the
Interaction Lab,
the
Robotics and Embedded Systems Lab,
or the
USC Robotics Research Lab.
by
Torbjørn S Dahl.