| Post-Stroke Assistive Robotics |
| Pioneer and Bandit Robot Configuration Movement Analysis |
| Motivation |
 |
 |
This
project lies in the post-stroke rehabilitation domain
and focuses on social human-robot interaction in order
to better provide the necessary therapy
to patients. While the upper torso Bandit robot tries
to administer post-stroke therapy to patients, a necessary
interaction and life-like movement
is required. This type of movement requires smooth
transitions and travel of the robot in order to emulate
human behavior and obtain
positive reactions and results from the patients themselves. |
| Methods |
 |
When
developing the method to solve the robot movement problem,
a more general approach was taken in order to obtain
both individual robot
configuration results as well as a more applicable
process to apply to other robot configuration and movement
requirements. In order to achieve this
greater applicability, a motor model and testing was
done. In addition a center of mass model was made in
order to find the system center
of mass for any unique robot configuration. Combining
these different models, a more general analysis of
any Pioneer base and upper torso Bandit robot configuration
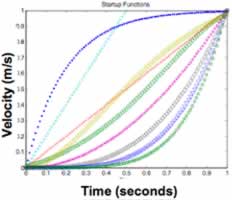
was achieved. An example of the velocity profiles used
to test the Pioneer base robot can be seen in Figure
1. An example center of mass model for a 56" upper
torso Bandit robot can be seen in Figure 2. |
| Figure 1 - Test Velocity Profiles | Figure 2 - Center of Mass Model |
 |  |
|
| Implementation |
 |
The
motors that turn the wheels on the Pioneer base robot
base are two Pittman 19.7:1 ratio DC motors. After
an initial motor model
was found, a series of nine different velocity profiles,
which can again be seen in Figure 1 above, were used
to test the motors. Using these velocity profiles,
an appropriate velocity profile was found that allowed
for smooth Pioneer base and upper torso
Bandit robot movement while staying within the limitations
of the other robotic hardware and software components.
For
each possible component in the Pioneer and Bandit
system, a series of tipping and weight tests were done
in order to
calculate each component’s center of mass. This center of mass
model was calculated to be a single mass point in
a three dimensional plane. By finding
the center of mass of each individual component,
the overall center of mass could then be calculated
regardless of arrangement of system. This center
of mass implementation allows for
robot design change and better accuracy.
This lead to the calculation of maximum
acceleration and deceleration of the
particular configuration in which the robot remains
stable and does not tip.
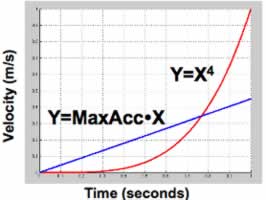
Figure 3 below shows the final results of the velocity
profile and center of mass tests. The velocity profile y = x^4 was used on the
robot configuration until maximum acceleration or deceleration was met, in which
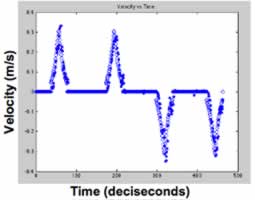
case the robot follows the y = MaxAcc•x curve. Figure 4 below shows actual results
of this type of velocity curve movement. The results show that the robot very
accurately follows the given velocity commands and demonstrated smooth movement
and transitions.
|
| Figure 3 - Theoretical Results | Figure 4 - Actual Results |
 |  |
|
| Application |
 |
Using
the motor and center of mass model, an accurate velocity
profile and maximum acceleration was found for the
configuration in Figure 2.
The applicability of these two models is widespread
since they can be used in any configuration. Figure
2 represents the approximate points found
in the system for the center of mass model. Figure
3 shows the theoretical velocity profile for which
any robot configuration would
take. The robot would travel along the function y =
x^4 until meeting the y=MaxAcc•X function. At this point, the robot
travels along this linear function to avoid acceleration
over its maximum limit. In demonstration, the
different robot configurations performed best with
the y = x^4 velocity profile on both startup and slow
down. The results and diagrams from the various tests
prove that the center of mass and motor models are
accurate. Because of their widespread applicability,
these models and procedures
can be further implemented and used on any robot configuration
in the lab in future experiments whenever smooth motion
is required. |
|
|
 |
|












